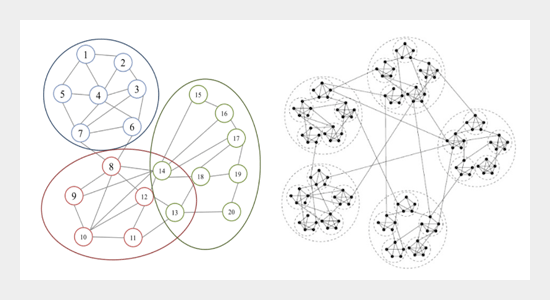
REFERENCES
- Agarwal, G., Kempe, D. 2008. Modularity-maximizing graph communities via mathematical programming, Eur. Phys. J. B, 66.
- Aloise, D., Cafieri, S., Caporossi, G., Hansen, P., Perron, S., Liberti, L. 2010. Column generation algorithms for exact modularity maximization in networks, Phys. Rev. E, 82.
- Andreev K., Räcke, H. 2006. Balanced graph partitioning, Theory of Computing Systems, 39, 929–939.
- Barabási, Albert-László, Albert, Réka, 1999. Emergence of scaling in random networks, Science, 286, 509–512.
- Blondel, V.D., Guillaume, J.L., Lambiotte, R., Lefebvre, E. 2008. Fast unfolding of communities in large networks, Statistical Mechanics: Theory and Experiment.
- Chakraborty, G. Sato, N. 2017. A reliable graph clustering method using genetic algorithm, International Symposium on Nonlinear Theory and Applications, Cancun, Mexico, December.
- Clauset, A., Newman, M.E.J., Moore, C. 2004. Finding community structure in very large networks, Physical Review, 066111.
- Dahlhaus, E., Johnson, D.S., Papadimitriou, C.H., Seymour, P.D., Yannakal, M. 1992. The complexity of multiway cuts (Extended Abstract), 24th. Annual ACM STOC, 241–251.
- Dinh, T.N., Li X., Thai, M.T. 2015. Network clustering via maximizing modularity: Approximation algorithms and theoretical limits, 2015 IEEE International Conference on Data Mining, Atlantic City, NJ, 101–110.
- Erdős, P., Rényi, A., 1959. On random graphs, Publicationes Mathematicae, 6, 290–297.
- Fiedler, M. 1975. A property of eigenvectors of nonnegative symmetric matrices and its application to graph theory, Czechoslovak Mathematical Journal, 25, 619–633.
- Fouss, F., Pirotte, A., Renders, J.M., Saerens, M. 2007. Random-Walk computation of similarities between nodes of a graph with application to collaborative recommendation, IEEE trans. On Knowledge and Data Engineering, 19, 355–369.
- Gergely, P., Imre, D., Illes, F., Tamas, V. 2005. Uncovering the overlapping community structure of complex networks in nature and society, Nature, 435, 814–818.
- Ghosal, A.K., Das, N., Bhattacharjee, S., Chakraborty, G. 2019. A fast parallel genetic algorithm based approach for community detection in large Networks, 11th International Conference on Communication Systems and Networks (COMSNETS2019), Bengaluru, India.
- Gleiser, P., Danon, L. 2003. Community structure in jazz, Advances in Complex Systems, 6, 565–573.
- Hafez, A.I. Ghali, N.I. Hassanien, A.E., Fahmy, A.A. 2012. Genetic algorithms for community detection in social networks, in 12th International Conference on Intelligent Systems Design and Applications (ISDA), 460–465.
- Karypis, G., Aggarwal, R., Kumar, V., Shekhar, S. 1970. Multilevel hypergraph partitioning: Applications in VLSI domain, IEEE Transactions on Very Large Scale Integration (VLSI) Systems, 7, 69–79.
- Kernighan, B.W., Lin, S. 1970. An efficient heuristic procedure for partitioning graphs, Bell System Technical Journal, 49, 291–307.
- Koblenz Network, 2013. Available: http://konect.uni-koblenz.de/.
- Li, Y., Liu, G., Lao, S.Y. 2013. A genetic algorithm for community detection in complex networks, Central South University, 20, 1269–1276.
- Lu, Y.C., Chakraborty, G. 2019. Definition and goal of graph clustering motivation to explore a new Algorithm,” ICAST conference, Japan.
- Lu, Y.C., Chakraborty, G. 2020. Improving efficiency of graph clustering by genetic algorithm using multi-objective optimization, IJASE journal.
- Lu, Y.C., Chakraborty, G., March, 2019. An efficient graph clustering algorithm using multiobjective pareto optimization, Advance Information Technology, 29–30 Taichung, Taiwan.
- Lusseau, D. 2003. The emergent properties of a dolphin social network, Proc. of the Royal Society of London B, 270, 186–188.
- Matsuo, Y. 2003. Prediction and discovering small world network, Society of Artificial Intelligence (in Japanese), 18.
- Matsuo, Y. 2005. Network structure and its emergence, Proceedings of AAAI, 11–14.
- Newman, M.E.J. 2006. Modularity and community structure in networks, Proceedings of the National Academy of Sciences, 103.
- Newman, M.E.J. 2010. Networks: An introduction, Oxford.
- Pons, P., Latapy, M. 2006. Computing communities in large networks using random walks, Graph Algorithms and Applications, 10, 191–218.
- Pothenf, A., Simon, H.D., Liou, K.P. 1990. Partitioning sparse matrices with eigenvectors of graphs, Industrial and Applied Mathematics, 11, 430–452.
- Rossi, R., Ahmed, N.K., Koh, E., Kim, S. 2019. Linear-time hierarchical community detection, https://arxiv.org/pdf/1906.06432.pdf.
- Schaeffer, S.E. 2007. Graph dlustering, Computer Science Review, 1, 27–64.
- Shang, R., Bai, J., Jiao, L., Jin, C. 2013. Community detection based on modularity and an improved genetic algorithm, Physica A: Statistical Mechanics and its Applications, 392, 1215–1231.
- Shi, J., Malik, J. 2000. Normalized cuts and image segmentation. Pattern Analysis and Machine Intelligence”, IEEE Transactions on, 22, 888–905.
- Šíma, J., Schaeffer, S.E. 2006. On the np-completeness of some graph cluster measures. In SOFSEM 2006: Theory and Practice of Computer Science, 530–537.
- Song, Y., Li, J., Zhang, X., Liu, C. 2012. Community detection using parallel genetic algorithms, Fifth International Conference on Advanced Computational Intelligence (ICACI), 374–378.
- Telesford, Q.K., Joyce, K.E., Hayasaka, S., Burdette, J.H., Laurienti, P.J. 2011. The ubiquity of small-world networks, Brain Connect, 1, 67–375.
- Watts, D.J., Strogatz, S.H., 1998. Collective dynamics of ’Small-World’ networks, Nature, 393.