Vasant A. Matsagar and R. S. Jangid* Department of Civil Engineering, Indian Institute of Technology Bombay, Powai, Mumbai - 400 076, India
Download Citation:
|
Download PDF
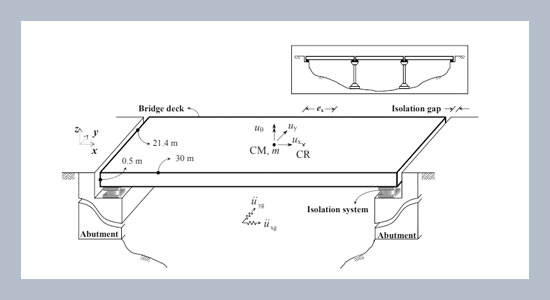
The seismic response of simply supported base-isolated bridge with different isolators is presented. The isolated bridge deck is idealized using simplified model of a simply supported rigid deck with three degrees-of-freedom, two lateral translational, mutually orthogonal and one rotational. The rotational degree-of-freedom of the bridge deck may arise because of the dissimilarity in properties of different seismic isolation devices such as elastomeric and sliding systems supporting the bridge deck. The sources of dissimilarity in the isolators considered here are the isolation stiffness and the yield force. The flexibility of abutments and bridge deck is ignored and two horizontal components of earthquake ground motion are applied, considering bi-directional interaction of the seismic response. The governing equations of motion for the uncoupled and torsionally coupled bridge are derived and solved using Newmark’s method of integration to obtain the seismic response. The parametric studies are conducted for different system configurations, isolation systems and frequency ratios during torsionally coupled and uncoupled conditions. The seismic response of base-isolated bridge is seen to be considerably altered due to the dissimilarity in the isolator properties. The eccentricity arose due to the isolation stiffness affects more than that due to the isolator yield forces. The effectiveness of isolation reduces at higher eccentricities and the torsionally coupled response diminishes with the increase of uncoupled torsional to lateral frequency ratio.ABSTRACT
Keywords:
asymmetry; base isolation; bridge; earthquake; eccentricity; torsional coupling.
Share this article with your colleagues
[1] Ghobarah, A. and Ali, H.M. 1988. Seismic Performance of Highway Bridges. Engineering Structures, 10(3), 157-166REFERENCES
[2] Turkington, D.H., Carr, A.J., Cooke, N. and Moss, P.J. 1988. Seismic Design of Bridges on Lead-Rubber Bearings. Journal of Structural Engineering, ASCE, 115, 3000-3016.
[3] Hwang, J.S. and Sheng, L.H. 1994. Equivalent Elastic Seismic Analysis of Base-Isolated Bridges with Lead-Rubber Bearings. Engineering Structures, 16(3), 201-209.
[4] Kartoum, A., Constantinou, M.C., and Reinhorn, A.M. 1992. Sliding Isolation System for Bridges: Analytical Study. Earthquake Spectra, 8(3), 345-372.
[5] Wang, Y.P., Chung, L.L., and Liao, W.H. 1998. Seismic Response Analysis of Bridges Isolated with Friction Pendulum Bearings. Earthquake Engineering and Structural Dynamics, 27(10), 1069-1093.
[6] Jangid, R.S. 2004. Seismic Response of Isolated Bridges. Journal of Bridge Engineering, ASCE, 9(2), 156-166.
[7] Kunde, M.C. and Jangid, R.S. 2003. Seismic Behavior of Isolated Bridges: A State-of-the-Art Review. Electronic Journal of Structural Engineering, 3, 140-170.
[8] Jangid, R.S. 1996. Seismic Response of an Asymmetric Base Isolated Structure. Computers and Structures, 60(2), 261-267.
[9] Jangid, R.S. 2000. Seismic Response of Structures with Sliding Systems. Journal of Seismology and Earthquake Engineering, 2(2), 45-54.
[10] Jangid, R.S. and Kelly, J.M. 2000. Torsional Displacements in Base-Isolated Buildings. Earthquake Spectra, 16(2), 443-454.
[11] Ryan, K.L. and Chopra, A.K. 2004. Estimation of Seismic Demands on Isolators in Asymmetric Buildings using Non-Linear Analysis. Earthquake Engineering and Structural Dynamics, 33(3), 395-418.
[12] Kunde, M.C. and Jangid, R.S. 2006. Effects of Pier and Deck Flexibility on the Seismic Response of Isolated Bridges, Journal of Bridge Engineering, ASCE, 11(1), 109-121.
[13] Matsagar, V.A. 2005. Earthquake Behavior and Impact Response Control of Base-Isolated Buildings. PhD Thesis, Indian Institute of Bombay, India.
[14] Simo, J.C. and Kelly, J.M. 1984. The Analysis of Multilayer Elastomeric Bearings. Journal of Applied Mechanics, ASME, 51(2), 244-250.
[15] Skinner, R.I., Kelly, J.M. and Heine, A.J. 1975. Hysteretic Dampers for Earthquake-Resistant Structures. Earthquake Engineering and Structural Dynamics, 3(3), 287-296.
[16] Robinson, W.H. Lead-Rubber Hysteretic Bearings Suitable for Protecting Structures During Earthquakes. Earthquake Engineering and Structural Dynamics, 10(4), 593-604.
[17] Park, Y.J., Wen, Y.K., and Ang, A.H.-S. 1986. Random Vibration of Hysteretic Systems under Bi-Directional Ground Motions. Earthquake Engineering and Structural Dynamics, 14(4), 543-557.
[18] Nagarajaiah, S., Reinhorn, A.M., and Constantinou, M.C. 1991. Nonlinear Dynamic Analysis of 3-D Base-Isolated Structures. Journal of Structural Engineering, ASCE, 117 (7), 2035-2054.
[19] Jangid, R.S. and Datta, T.K. 1994. Nonlinear Response of Torsionally Coupled Base Isolated Structure. Journal of Structural Engineering, ASCE, 120(1), 1-22.
[20] Zayas, V.A, Low, S.S., and Mahin, A. 1990. A Simple Pendulum Technique for Achieving Seismic Isolation. Earthquake Spectra, 6(2), 317-333.
ARTICLE INFORMATION
Accepted:
2006-03-07
Available Online:
2006-04-04
Matsagar, V.-A., Jangid, R.-S. 2006. Seismic response of simply supported Base-Isolated bridge with different isolators. International Journal of Applied Science and Engineering, 4, 53–69. https://doi.org/10.6703/IJASE.2006.4(1).53
Cite this article: