Mohammad Sajida* and Abdullah S. Alsuwaiyanb aMechanical Engineering Department, College of Engineering Qassim University, Buraidah, Qassim, Saudi Arabia
bMechanical Engineering Department, Unayzah College of Engineering Qassim University, Saudi Arabia
Download Citation:
|
Download PDF
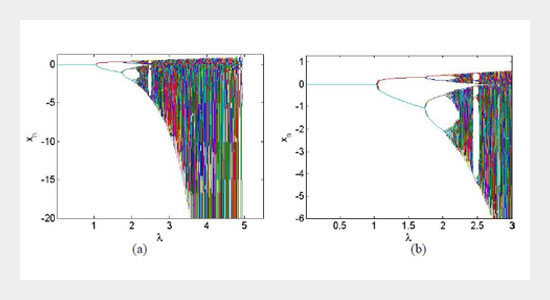
The chaotic behavior in the real dynamics of a one parameter family of nonlinear functions is studied in the present paper. For this purpose, the function fλ (x) = λ· xex /( x - 1 ) λ> 0, x ∈ R \ {1} is considered. The fixed points, periodic points and their nature are investigated for the function fλ (x). Bifurcation is shown to occur in the dynamics of fλ (x). Period doubling, which is a route of chaos in the real dynamics, is also shown to take place in the real dynamics of fλ (x). The orbits of the dynamics of fλ (x) are graphically represented by time series graphs. Moreover, the chaotic behavior in the dynamics of computing positive Lyapunov exponents.ABSTRACT
Keywords:
Bifurcation; chaos; dynamics; fixed point; Lyapunov exponents.
Share this article with your colleagues
[1] Kapitaniak, T. 2000. “Chaos for Engineers: Theory Applications & Control”. 2nd edn. Springer.REFERENCES
[2] Florian, S. 2010. “Mechanics: From Newton’s Laws to Deterministic Chaos”. 5th edn. Springer.
[3] Thompson, J. M. T. and Stewart , HB. 2002. “Nonlinear Dynamics and Chaos”. 2nd edn. John Wiley & Sons.
[4] Li, T. Y. and Yorke, J. A. 1975. Period Three Implies Chaos. The American Mathematical Monthly, 82, 10:985-992.
[5] Elaydi, S. N. 2011. “Discrete Chaos.” 2nd edn. Chapman and Hall/CRC.
[6] Alligood, K. T., Sauer, T. D., and Yorke, J. A. 1997. “Chaos: An Introduction to Dynamical Systems”. Springer.
[7] Lakshmanan, M. and Rajaseekar, S. 2003. “Nonlinear Dynamics: Integrability, Chaos and Patterns”. Springer.
[8] Manneville, P. 2004. “Instabilities, Chaos and Turbulence: An Introduction to Nonlinear Dynamics and Complex Systems”. World Scientific Publishing Co.
[9] Devaney, R. L. 1992. “A First Course in Chaotic Dynamical Systems”. Westview Press.
[10] Thunberg, H. 2001. Periodicity versus Chaos in One-Dimensional Dynamics. SIAM REVIEW, 43, 1:3-30.
[11] Xingyuan, W. and Qingyong, L. 2008. Reverse bifurcation and fractal of the compound logistic map. Comm. Nonlinear Sci. & Numerical Simul, 13, 913-927.
[12] Maier, M. P. S. and Peacock-López, E. 2010. Switching induced oscillations in the logistic map. Physics Letters A, 374, 1028–1032.
[13] Stavroulaki, M. and Sotiropoulos, D. 2012. The Energy of Generalized Logistic Maps at Full Chaos. Chaotic Modeling and Simulation, 3, 543-550.
[14] Yang, X. S. 2007. “Applied Engineering Mathematics”. Cambridge Int. Science Publishing.
[15] Devaney, R. L. 1991. e^z: Dynamics and Bifurcations. Int. J. Bifur. Chaos, 1, 287–308.
[16] Schleicher, D. and Zimmer, J. 2003. Escaping Points of Exponential Maps. Journal of the London Mathematical Society, 67, 2: 380-400.
[17] Devaney, R. L. 2010. Complex Exponential Dynamics. In Broer, H., Takens, F., and Hasselblatt, B., eds., Handbook of Dynamical Systems, 3, 125-224.
[18] Devaney, R. L. and Rocha, M. M. 2002. A Semilinear Model for Exponential Dynamics and Topology. Topology Proceedings, 26, 153-167.
[19] Badeńska, A. 2011. Misiurewicz parameters in the exponential family. Mathematische Zeitschrift, 268, 1-2: 291-303.
[20] Abu-Amara, F. and Musa, A. August 2012. Robust Chaos via Smooth Exponential Map. Int. Journal of Future Computer and Communication, 1, 2: 196-198.
[21] Stumpf, L. 1999. Chaotic behaviour in the newton iterative function associated with kepler's equation. Celestial Mech. and Dynamicall Astro., 74, 2: 95-109.
[22] Deshpande, V. S., Needleman, A., and Giess, E. V. d. 2001. Dislocation dynamics is chaotic. Scripta Materialia, 45, 1047-1053.
ARTICLE INFORMATION
Received:
2013-11-23
Revised:
2014-06-11
Accepted:
2014-07-09
Available Online:
2014-12-01
Sajid, M., Alsuwaiyan, A.S. 2014. Chaotic behavior in the real dynamics of a one parameter family of functions. International Journal of Applied Science and Engineering, 12, 289–301. https://doi.org/10.6703/IJASE.2014.12(4).289
Cite this article: