Abdulnaser M. Alshoaibi* Department of Mechanical Engineering, Jazan University, Jazan, Kingdom of Saudi Arabia
Download Citation:
|
Download PDF
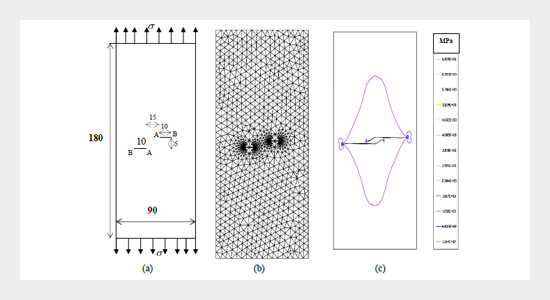
An adaptive Finite Element framework for fatigue crack propagation analysis under constant amplitude loading is proposed. This framework combines the simplicity of standard industrial fatigue crack propagation analysis with the generality and accuracy of a full Finite Element analysis and can be implemented by combining standard existing computational tools. The equivalent domain integral method has been used to predict the fatigue crack direction as well as the corresponding stress-intensity factors is estimated at each small crack increment. The propagation is modeled by successive linear extensions, which are determined by the stress intensity factors under linear elastic assumption. The procedure is applied to the fatigue analysis of two internal parallel cracks specimen. The fatigue life cycle analysis is based upon Paris’ equation. The proposed methodology is implemented in an interactive graphics computational scheme for 2D finite element analysis, which includes modeling, analysis, and visualization capabilities. The numerical results are validated with other relevant researcher’s results.ABSTRACT
Keywords:
Finite element; fatigue crack propagation; adaptive mesh; constant amplitude loading; stress intensity factor.
Share this article with your colleagues
[1] Portela, A., Aliabadi, M., Rooke, D. P. 1991. The dual boundary element method: effective implementation for crack problem. International Journal for Numerical Methods in Engineering, 33, 6: 1269–1287.REFERENCES
[2] Yan, A.M. and Nguyen-Dang, H. 1995. Multiple-cracked fatigue crack growth by BEM. Computational Mechanics, 16, 5: 273–280.
[3] Yan, X. 2006. A boundary element modeling of fatigue crack growth in a plane elastic plate. Mechanics Research Communications, 33, 4: 470–481.
[4] Belytschko, T., Gu, L., Lu, Y. Y. 1994. Fracture and crack growth by element-free Galerkin methods. Modelling and Simulation in Materials Science and Engineering, 2, 3A: 519–534.
[5] Belytschko, T., Lu, Y.Y., and Gu, L. 1995. Crack propagation by element-free Galerkin methods. Engineering Fracture Mechaincs, 51, 2: 295–315.
[6] Duflot, M. and Nguyen-Dang, H. 2004. A meshless method with enriched weight functions for fatigue crack growth. International Journal for Numerical Methods in Engineering, 59, 14: 1945–1961.
[7] Duflot, M. and Nguyen-Dang, H. 2004. Fatigue crack growth analysis by an enriched meshless method. Journal of Computational and Applied mathmatics, 168,1-2: 155–164.
[8] Miranda, A.C.O., Meggiolaro, M.A., Castro, J.T.P., Martha, L.F. and Bittencourt, T.N., 2003. Fatigue life and crack path predictions in generic 2D structural components. Engineering Fracture Mechanics, 70: 1259–1279
[9] Alshoaibi, A. M. 2010. Finite Element Procedures for the Numerical Simulation of Fatigue Crack Propagation under Mixed Mode Loading. Structural Engineering and Mechanics, 35, 3: pp.283-299.
[10] Löhner, R. 1997. Automatic unstructured grid generators. Finite Element in Analysis and Design, 25, 1-2: 111-134.
[11] Zienkiewicz, O.C., Taylor, R.L. and Zhu, J.Z. 2005. The finite element method: its basis and fundamentals. 6th Edition, Elsevier Butterworth-Heinemann.
[12] Alshoaibi, M. Abdulnaser, Hadi, M.S.A. and Ariffin, A.K., 2007 . An adaptive finite element procedure for crack propagation analysis. Journal of Zhejiang University of Science: An International Journal of Applied Physics and Engineering, 8, 2: 228-236.
[13] Bazant, Z. P. and Planas, J. 1998. Fracture and Size Effect in Concrete and Other Quasibrittle Materials. Boca Raton, FL: CRC Press.
[14] Ingliss, C. E. 1913. Stress in a plate due to the presence of cracks and sharp corners. Trans. Institute of Naval Architects 55, 219-241.
[15] Griffith, A.A. 1920. The phenomena of rupture and flow in solids. Philosophical Transactions of the Royal Society 221: 163–198.
[16] Irwing, G. R. 1957. Analysis of stress and strain near the end of a crack traversing a plate. Journal of Applied Mechanics ASME, 24, 361-364
[17] Alshoaibi, M. A. 2013. Adaptive finite element modeling of fatigue crack propagation. International Journal of Materials Science and Applications, 2, 3: 104-108
[18] Bittencourt, T.N., Wawrzynek, P.A., Ingraffea, A.R., and Sousa, J.L. 1996. Quasi-automatic simulation of crack propagation for 2D LEFM problems. Engineering Fractrue Mechanics, 55, 2: 321-334.
[19] Erdogan, F. & Sih, G. 1963. On the crack extension in plates under plane loading and transverse shear. Journal of Basic Engineering 85: 519–27.
[20] Tu, S.T. and Cai, R.Y. 1993. A coupling of boundary elements and singular integral equation for the solution of the fatigue cracked body. Stress Analysis, pp. 239–247.
ARTICLE INFORMATION
Received:
2014-10-29
Revised:
2015-10-20
Accepted:
2015-10-28
Available Online:
2015-09-01
Alshoaibi, A.M. 2015. An adaptive finite element framework for fatigue crack propagation under constant amplitude loading. International Journal of Applied Science and Engineering, 13, 261–270. https://doi.org/10.6703/IJASE.2015.13(3).261
Cite this article: