Download Citation:
|
Download PDF
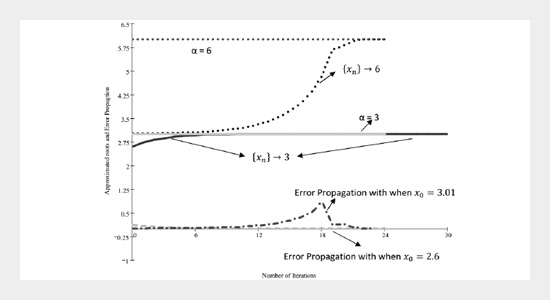
In this paper the convergence behavior of a variant of Newton’s method based on the root mean square for solving nonlinear equations is proposed. The convergence properties of this method for solving non linear equations which have simple or multiple roots have been discussed and it is shown that it converges cubically to simple roots and linearly to multiple roots. Moreover, the values of the corresponding asymptotic error constants of convergence are determined. Theoretical results have been verified on the relevant numerical problems. A comparison of the efficiency of this method with other mean-based Newton’s methods is also included. Convergence behavior and error equations are also exhibited graphically for comparison on considering a particular example.ABSTRACT
Keywords:
Numerical analysis; nonlinear equations; iterative methods; root mean square; order of convergence; asymptotic error constants.
Share this article with your colleagues
REFERENCES
ARTICLE INFORMATION
Received:
2014-05-02
Revised:
2016-05-30
Accepted:
2016-06-03
Available Online:
2016-07-01
Verma, K.L. 2016. References on a variant of newton’s method for simple and multiple roots of non linear equations. International Journal of Applied Science and Engineering, 14, 101–114. https://doi.org/10.6703/IJASE.2016.14(2).101
Cite this article: