Chun-Chin Hsu1*, Chun-Yuan Cheng1, Fang-Chih Tien2 1 Department of Industrial Engineering and Management, Chaoyang University of Technology, Taichung, Taiwan, R.O.C.
2 Department of Industrial Engineering and Management, National Taipei University of Technology, Taipei, Taiwan, R.O.C.
Download Citation:
|
Download PDF
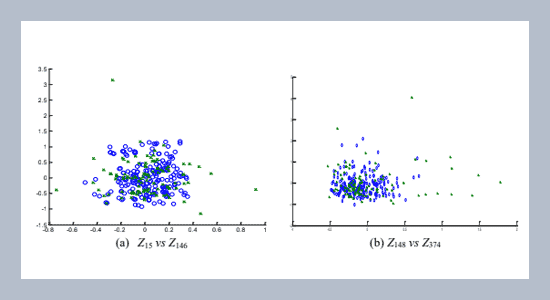
As the growth of Industry 4.0, online fault detection plays a crucial role in ensuring the manufacturing quality. Generally, the fault detection methods can be classified into model-based and data-driven methods. There are advantages/disadvantages between two methods. In this study, we integrated both methods in order to develop an efficient fault detection method for non-Gaussian industrial processes. The data-driven method, independent component analysis (ICA) is used to extract non-Gaussian information and dimensionality reduction. Meanwhile, the model-based method, generalized likelihood ratio (GLR) test is adopted as the charting statistic. The proposed ICA-GLR method has advantages of 1) detecting a wide range of process changes, 2) estimating the change points and 3) needless prior parameters to be specified by practitioner. The efficiency of the proposed ICA-GLR fault detection method will be verified via implementing one simulated non-Gaussian process and two real manufacturing processes: Tennessee Eastman process and semiconductor manufacturing process. Results demonstrate that the proposed ICA-GLR method has superior fault detectability when compared to traditional methods, such as principal component analysis and ICA.ABSTRACT
Keywords:
Fault detection, Principal component analysis, Independent component analysis, Generalized likelihood ratio test, Non-Gaussian.
Share this article with your colleagues
REFERENCES
ARTICLE INFORMATION
Received:
2020-12-17
Revised:
2021-02-23
Accepted:
2021-03-23
Available Online:
2021-06-01
Hsu, C.-C., Cheng, C.-Y., Tien, F.-C. 2021. Fault detection based on ICA-GLR for non-Gaussian industrial processes, International Journal of Applied Science and Engineering, 18, 2020332. https://doi.org/10.6703/IJASE.202106_18(2).015
Cite this article:
Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.