Jabbar. H. Mohmmed*, Mauwafak A. Tawfik, Qasim Abbas Atiyah Mechanical Engineering Department, University of Technology Industrial St., Al-Karrada City, Baghdad Province, Iraq
Download Citation:
|
Download PDF
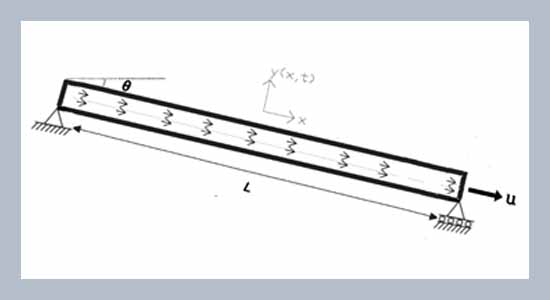
This study treats with the transverse vibration of polypropylene random-copolymer (PP-R) pipes caused by fluid flow inside them assuming pinned connections at both ends. The effect of inclination angle, aspect ratio (the ratio of length to outside diameter) and temperature variation on dynamic response of inclined pipe containing flowing fluid with different velocity was investigated. The Euler–Bernoulli formula for beam theory was adopted to model the inclined pipe. An analytical model has been prepared to calculate the dynamic response of the pipe, taking into account pipe weight, thermal effect, inclination angle, aspect ratio, and fluid flow velocity, using the integral transform techniques (ITT) by utilizing a combining of Laplace and Fourier transforms and their inverses. The results demonstrate that the prepared analytic model is a powerful tool to obtain the dynamic characteristic of pipe conveying fluid. Moreover, the results showed that the dynamic deflection was strongly affected by the change in the values of inclination angle, pipe temperature, aspect ratio, and fluid velocity, where there was a significant increase in pipe deflection with increasing temperature and aspect ratio. and fluid velocity, while a decrease in the deflection value is observed with an increase in the angle of inclination in the range of 0-90°. The findings proved that the thermal effect becomes more important than the fluid velocity at high aspect ratios. The same case applies to the angle of inclination, as its effect on the pipe deflection increases at high aspect ratios. These results were limited to the fundamental (first) mode and can be useful for engineering component design. The main contributions of this work are to find the combined effect of inclination angle, thermal loading, and aspect ratio on the deflection of the pipe, in addition to preparing an analytical model to calculate this deflection.ABSTRACT
Keywords:
Flow velocity, Dynamic response, Temperature variation, Finite Fourier sine transforms, Laplace transforms, inclined pipe conveying fluid.
Share this article with your colleagues
REFERENCES
ARTICLE INFORMATION
Received:
2021-05-11
Revised:
2021-08-25
Accepted:
2021-09-07
Available Online:
2021-12-01
Mohmmed, J.H., Tawfik, M.A., Atiyah, Q.A. 2021. Dynamic response of inclined pipe conveying fluid under thermal effect. International Journal of Applied Science and Engineering, 18, 2021133. https://doi.org/10.6703/IJASE.202112_18(6).003
Cite this article:
Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.