Gashu Gadisa, Gemechis File* and Tesfaye Aga Department of Mathematics, Jimma University, Jimma, Ethiopia
Download Citation:
|
Download PDF
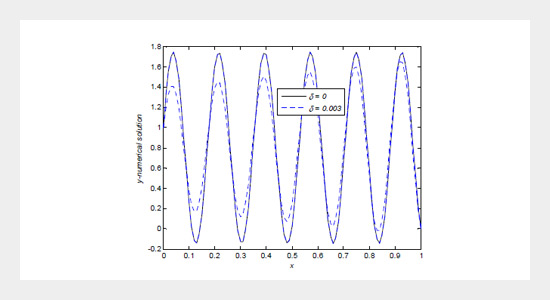
This paper presents a numerical method to solve singularly perturbed delay differential equations. The solution of this problem exhibits layer or oscillatory behaviour depending on the sign of the sum of coefficients in reaction terms. A fourth order finite difference scheme on a uniform mesh is developed. The stability and convergence of the proposed method have been established. The effect of delay parameter (small shift) on the boundary layer(s) has also been analyzed and depicted in graphs. The applicability of the proposed scheme is validated by implementing it on four model examples. To show the accuracy of the method, the results are presented in terms of maximum absolute errors.ABSTRACT
Keywords:
Singular perturbation; delay differential equation; boundary layer.
Share this article with your colleagues
[1] Kokotovic, P., Khalil, H.K. and O’Reilly, J. 1986. “Singular Perturbation Methods in Control: Analysis and Design”. Academic Press, New York. doi: 10.1137/1.9781611971118REFERENCES
[2] Stein, R. B. 1967. Some models of neuronal variability. Biophysical Journal, 7, 1: 37–68. doi.org/10.1016/S0006-3495(67)86574-3
[3] Stein, R. B. 1965. A theoretical analysis of neuronal variability. Biophysical Journal, 5, 2: 173–194. doi: 10.1016/S0006-3495(65)86709-1
[4] Doolan, E. P., Miller, J. J. H. and Schilders, W.H.A. 1980. “Uniform Numerical Methods for Problems with Initial and Boundary Layers”. Boole Press, Dublin.
[5] Kadalbajoo, M. K. and Reddy, Y. N. 1989. Asymptotic and numerical analysis of singular perturbation problem: A survey. Applied Mathematics and Computation, 30, 3: 223-259. doi: 10.1016/0096-3003(89)90054-4
[6] Roos, H. G., Stynes, M. and Tobiska, L. 1996. “Numerical Methods for Singularly Perturbed Differential Equations: Convection-Diffusion and Flow Problems”. Springer-Verlag, doi.org/10.1007/978-3-662-03206-0
[7] File, G., Gadisa, G., Aga, T. and Reddy, Y. N. 2017. Numerical solution of singularly perturbed delay reaction-diffusion equations with layer or oscillatory behavior. American Journal of Numerical Analysis, 5, 1:1-10. doi: 10.12691/ajna-5-1-1
[8] Ramesh, V. P. and Kadalbajoo, M. K. 2011. Numerical algorithm for singularly perturbed delay differential equations with layer and oscillatory behavior. Neural, Parallel, and Scientific Computations, 19, 1-2: 21-34.
[9] Rao, R. N. and Chakravarthy, P. P. 2013. A finite difference method for singularly perturbed differential difference equations with layer and oscillatory behavior. Applied Mathematical Modelling, 37, 8: 5743–5755. doi: 10.1016/j.apm.2012.11.004
[10] Swamy, D. K., Phaneendra, K., Babu, A. B. and Reddy, Y. N. 2015. Computational method for singularly perturbed delay differential equations with twin layers or oscillatory behavior. Ain Shams Engineering Journal, 6, 1: 391–398. doi.org/10.1016/j.asej.2014.10.004
[11] Kadalbajoo, M. K. and Ramesh, V. P. 2007. Numerical methods on Shishkin mesh for singularly perturbed delay differential equations with a grid adaptation strategy. Applied Mathematics and Computation, 188, 2: 1816–1831. doi: 10.1016/j.amc.2006.11.046
[12] Rai, P., Sharma, K. K. 2011. Numerical analysis of singularly perturbed delay differential turning point Applied Mathematics and Computation, 218, 7: 3483-3498. doi.org/10.1016/j.amc.2011.08.095
[13] El’sgol’ts, L. E. and Norkin, S. B. 1973. “Introduction to the Theory and Applications of Differential Equations with Deviating Arguments”. Academic Press, New York.
[14] O’Riordan, E. and Stynes, M. 1991. A globally uniformly convergent finite element method for a singularly perturbed elliptic problem in two dimensions. Mathematics of Computation, 57, 195: 47-62.
[15] Varga, R.S. 1962. “Matrix Iterative Analysis”. Prentice-Hall. Englewood Cliffs, New Jersey.
[16] Young, D. M. and Rheinboldt, W. 1971. Iterative solution of large linear systems, Academic Press, Inc. New York.
ARTICLE INFORMATION
Received:
2016-10-10
Revised:
2017-10-15
Accepted:
2017-10-21
Available Online:
2018-02-01
Gadisa, G., File, G., Aga, T. 2018. Fourth order numerical method for singularly perturbed delay differential equations. International Journal of Applied Science and Engineering, 15, 17-32. https://doi.org/10.6703/IJASE.201802_15(1).017
Cite this article: