International Journal of Applied Science and Engineering
Published by Chaoyang University of Technology

Siva Manohar Reddy Kesu1*, Hariharan Ramasangu2

1 Faculty of Engineering and Technology, M S Ramaiah University of Applied Sciences, Bengaluru, India

2 Research Division, Relecura. Inc, Bengaluru, India

 

Download Citation: |
Download PDF


ABSTRACT

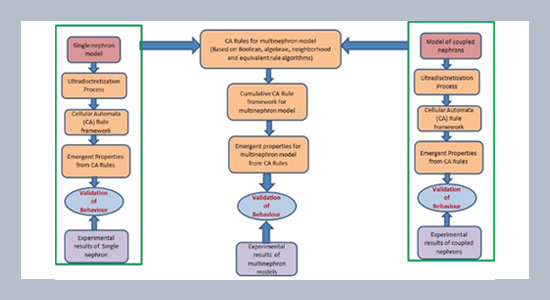
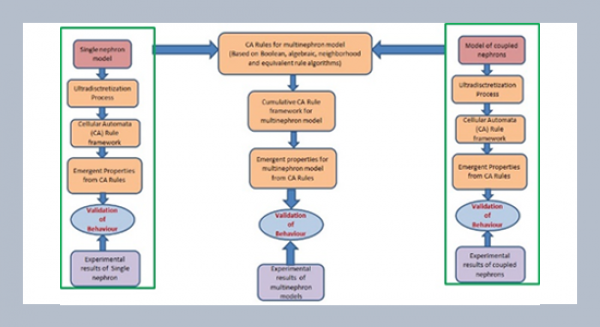
Developing a whole kidney model is important for effective diagnostic procedures and treating kidney diseases. The modeling of a multi-nephron network aids in developing the whole kidney model. The key aspect of any nephron model is understanding the pressure dynamics. The governing equations for pressure dynamics in the kidney depend on the number of nephrons and their interactions. There are mathematical models to analyze the local and global behaviors of single and coupled nephrons. It is difficult to formulate governing equations for a whole kidney model. This necessitates the development of simulation models. Even the simulation models have only been developed for 72 nephrons. The complexity is involved in incorporating both local and global behaviors of nephrons. In this paper, a cellular automata (CA) framework has been proposed to study the global behavior of nephrons. The advantage of the proposed CA framework is its scalability and its ability to capture global dynamics without formulating the corresponding governing equations. The limitation of the CA framework is its inability to compare point-to-point local behavior. But the clinical findings suggest that global behavior gives significant information about the kidney. We have developed CA rules for 8-nephron, 16-nephron, 72-nephron and 100-nephron network models considering both rigid and compliance tubules. The CA rules with various initialization schemes produce different evolutionary patterns similar to the emergent dynamical behavior of nephrons obtained from experimental and numerical findings. Evolutionary patterns of the CA framework are related to normotensive and hypertensive pressure dynamics. The in-phase and out-of-phase synchronizations have also been observed in the CA evolutionary patterns. The irregular rhythm of the cardiovascular system may give rise to shock waves in the pressure dynamics of the kidney. This behavior has also been observed in the proposed CA framework.


Keywords: Nephron-network, Cellular automata, Hypertension, Emergent properties.


Share this article with your colleagues

 


REFERENCES

  1. Beard, D.A., Mescam, M. 2012. Mechanisms of pressure-diuresis and pressure-natriuresis in Dahl salt-resistant and Dahl salt-sensitive rats. BMC Physiology, 12, 1.

  2. Bohr, H., Jensen, K.S., Petersen, T., Rathjen, B., Mosekilde, E., Holstein-Rathlou, N.-H. 1989. Parallel computer simulation of nearest-neighbour interaction in a system of nephrons. Parallel Computing, 12, 113–120.

  3. Isojima, S., Grammaticos, B., Ramani, A., Satsuma, J. 2006. Ultradiscretization without positivity. Journal of Physics A: Mathematical and General, 39, 3663.

  4. Kanzaki, G., Tsuboi, N., Shimizu, A., Yokoo, T. 2020. Human nephron number, hypertension, and renal pathology. The Anatomical Record, 303, 2537–2543.

  5. Keener, J.P., Sneyd, J. 1998. Mathematical physiology, 1, Springer.

  6. Kesu, S.M.R., Ramasangu, H. 2021a. Spatio-temporal evolution of cellular automata based single nephron rigid tubular model. The 12th International Conference on Computational Systems-Biology and Bioinformatics, 90–97.

  7. Kesu, S.M.R., Ramasangu, H. 2021b. Cellular automata based coupled nephron model for pressure-driven oscillations, 2021 IEEE 18th India Council International Conference (INDICON), 1–6.

  8. Kesu, S.M.R., Ramasangu, H. 2022. Cellular automata model for emergent properties of pressure flow in single nephron compliance tubule. Indonesian Journal of Electrical Engineering and Computer Science, 25, 1227.

  9. Khouhak, J., Faghani, Z., Jafari, S. 2019. Wave propagation in a network of interacting nephrons. Physica A: statistical mechanics and its applications, 530, 121566.

  10. Khouhak, J., Faghani, Z., Laugesen, J.L., Jafari, S. 2020. The emergence of chimera states in a network of nephrons. Chinese Journal of Physics, 63, 402–409.

  11. Laugesen, J.L. 2011. Modelling nephron autoregulation and synchronization in coupled nephron systems. (Doctoral dissertation, Technical University of Denmark (DTU)).

  12. Layton, A.T. 2021. His and her mathematical models of physiological systems. Mathematical Biosciences, 108642.

  13. Layton, A. T., Edwards, A. 2014. Mathematical Modeling in Renal Physiology. Springer.

  14. Marsh, D.J., Postnov, D.D., Sosnovtseva, O., Holstein-Rathlou, N.-H. 2019. The nephron-arterial network and its interactions. American Journal of Physiology-Renal Physiology, 316, F769–F784.

  15. Marsh, D.J., Sosnovtseva, O, Mosekilde, E., Holstein-Rathlou, N.-H. 2007. Vascular coupling induces synchronization, quasiperiodicity, and chaos in a nephron tree. Chaos: An Interdisciplinary Journal of Nonlinear Science, 17, 15114.

  16. Marsh, D.J., Wexler, A.S., Brazhe, A., Postnov, D.E., Sosnovtseva, O, Holstein-Rathlou, N.-H. 2013. Multinephron dynamics on the renal vascular network. American Journal of Physiology-Renal Physiology, 304, F88–F102.

  17. Matsuya, K., Murata, M. 2013. Spatial pattern of discrete and ultradiscrete Gray-Scott model. ArXiv Preprint ArXiv:1305.5343.

  18. Moss, R. 2008. A clockwork kidney: Using hierarchical dynamical networks to model emergent dynamics in the kidney. Doctoral dissertation, University of Melbourne, Department of Computer Science and Software Engineering.

  19. Moss, R., Kazmierczak, E., Kirley, M., Harris, P. 2009. A computational model for emergent dynamics in the kidney. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 367, 2125–2140.

  20. Moss, R., Layton, A.T. 2014. Dominant factors that govern pressure natriuresis in diuresis and antidiuresis: A mathematical model. American Journal of Physiology-Renal Physiology, 306, F952–F969.

  21. Moss, R., Thomas, S.R. 2014. Hormonal regulation of salt and water excretion: A mathematical model of whole kidney function and pressure natriuresis. American Journal of Physiology-Renal Physiology, 306, F224–F248.

  22. Murata, M. 2013. Tropical discretization: Ultradiscrete Fisher–KPP equation and ultradiscrete Allen–Cahn equation. Journal of Difference Equations and Applications, 19, 1008–1021.

  23. Ohmori, S., Yamazaki, Y. 2015. Cellular automata for spatiotemporal pattern formation from reaction–diffusion partial differential equations. Journal of the Physical Society of Japan, 85, 14003.

  24. Ravasz, E., Barabási, A.-L. 2003. Hierarchical organization in complex networks. Physical Review E, 67, 26112.

  25. Ryu, H. 2014. Feedback-mediated dynamics in the kidney: Mathematical modeling and stochastic analysis (Doctoral dissertation, Duke University).

  26. Ryu, H., Layton, A.T. 2014. Tubular fluid flow and distal NaCl delivery mediated by tubuloglomerular feedback in the rat kidney. Journal of Mathematical Biology, 68, 1023–1049.

  27. Thomas, G. 2016. Simulation of whole mammalian kidneys using complex networks. Doctoral dissertation, University of Melbourne, Parkville, Victoria, Australia.

  28. Tokihiro, T., Takahashi, D., Matsukidaira, J., Satsuma, J. 1996. From soliton equations to integrable cellular automata through a limiting procedure. Physical Review Letters, 76, 3247.

  29. Voorhees, B. 2012. Selfing dynamics in the rule space of additive cellular automata. International Journal of General Systems, 41, 609–616.

  30. Voorhees, B.H. 1996. Computational analysis of one-dimensional cellular automata, 15. World Scientific.
  31. Weisstein, E.W. 2002. Additive cellular automaton. https://mathworld.wolfram.com/.

  32. Ziganshin, A.R., Pavlov, A.N. 2005. Scaling properties of multimode dynamics in coupled chaotic oscillators. Proceedings. 2005 International Conference Physics and Control, 180–183. IEEE.


ARTICLE INFORMATION

Received: 2022-05-09
Revised: 2022-11-30
Accepted: 2023-03-11
Available Online: 2023-04-27


Cite this article:

Kesu, S.M.R., Ramasangu, H. Pressure flow dynamics in cellular automata based nephron network model. International Journal of Applied Science and Engineering, 20, 2022123. https://doi.org/10.6703/IJASE.202306_20(2).009

  Copyright The Author(s). This is an open access article distributed under the terms of the Creative Commons Attribution License (CC BY 4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are cited.

Other people also read ...

doaj logo

 

2.3
2022CiteScore
 
 
48th percentile
Powered by  Scopus
 
 

SCImago Journal & Country Rank

IJASE - Most Read Articles

IJASE - Most popular articles