International Journal of Applied Science and Engineering
Published by Chaoyang University of Technology

Peddi Phani Bushan Raoa,* and Nowpada Ravi Shankarb

a Department of Mathematics, GITAM Institute of Technology, GITAM University, Visakhapatnam, India
b Department of Applied Mathematics, GITAM Institute of Science, GITAM University, Visakhapatnam, India

 

Download Citation: |
Download PDF


ABSTRACT

This paper describes a ranking method for ordering fuzzy numbers based on area, mode, spreads and weights of generalized fuzzy numbers. The area used in this method is ob-tained from the generalized trapezoi-dal fuzzy number, first by splitting the generalized trapezoi dal fuzzy numbers into three plane figures and then calculating the centroids of each plane figure followed by the centroid of these centroids and then finding the area of this centroid from origin which is a process of defuzzification proposed in this paper. This method is simple in evalua-tion and can rank various types of fuzzy numbers and also crisp numbers which are considered to be a special case of fuzzy numbers.


Keywords: Ranking function; centroid points; generalized trapezoidal fuzzy numbers.


Share this article with your colleagues

 


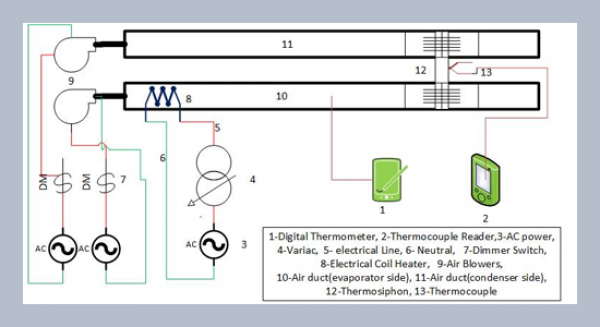
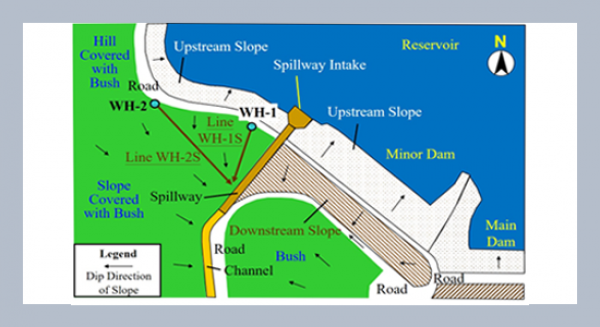
REFERENCES

  1. [1] Abbasbandy, S. and Hajjari, T. 2009. Anew approach for ranking of trapezoidal fuzzy numbers. Computers and Mathematicswith Applications, 57, 3: 413-419.

  2. [2] Abbasbandy, S. and Asady, B. 2006.Ranking of fuzzy numbers by sign distance. Information Sciences, 176:2405-2416.

  3. [3] Adamo, J. M. 1980. Fuzzy decision trees, Fuzzy Sets and Systems, 4: 207-219.

  4. [4] Baldwin, J. F. and Guild, N. C. F. 1979.Comparison of fuzzy numbers on thesame decision space. Fuzzy Sets andSystems, 2: 213-233.
  5. [5] Bortolan, G. and Degani, R. 1985. A reviewof some methods for ranking fuzzy subsets. Fuzzy Sets and Systems, 15:1-19.

  6. [6] Chen S. J. and Chen S. M. 2007. Fuzzyrisk analysis based on the ranking ofgeneralized trapezoidal fuzzy numbers, Applied Intelligence, 26 ,1: 1-11.

  7. [7] Chen, S. H. 1985. Ranking fuzzy numberswith maximizing set and minimiz-ing set, Fuzzy Sets and Systems, 17, 1:113-129.

  8. [8] Chen, S. M. and Chen, J. H. 2009. Fuzzyrisk analysis based on ranking general-ized fuzzy numbers with different heights and different spreads. ExpertSystems with Applications, 36, 3:6833-6842.

  9. [9] Cheng, C. H. 1998. A new approach forranking fuzzy numbers by distancemethod, Fuzzy Sets and Systems, 95, 3:307-317.

  10. [10] Chu, T. C. and Tsao, C. T. 2002. Ranking fuzzy numbers with an area between the Centroid point and original point, Com-puters and Mathematics with Applications, 43: 111-117.

  11. [11] Chu, T. C. and Tsao, C. T. 2002. Ranking fuzzy numbers with an area between the Centroid point and original point, Com-puters and Mathematics with Applications, 43: 111-117.

  12. [12] Dubois, D. and Prade, H. 1983. Rankingfuzzy numbers in the setting of possibilitytheory, Information Sciences, 30:183-224.

  13. [13] Fortemps, P. and Roubens, M. 1996.Ranking and defuzzification methods based on area compensation, Fuzzy Sets and Systems, 82: 319-330.

  14. [14] Garcia, M. S. and Lamata, M. T. 2007. A modification of the index of liou andwang for ranking fuzzy number, Interna-tional Journal of Uncertainty, Fuzzinessand Knowledge-Based Systems, 15, 4:411-424.

  15. [15] Jain, R. 1976. Decision making in the presence of fuzzy variables, IEEE Transactions on Systems, Man and Cy-bernetics, 6: 698-703.

  16. [16] Jain, R. 1978. A procedure for multi as-pect decision making using fuzzy sets, International Journal of systems sci-ence, 8: 1-7.

  17. [17] Kim, K.and Park, K. S. 1990. Ranking fuzzy numbers with index of optimism, Fuzzy Sets and Systems, 35: 143-150.

  18. [18] Kumar, A., Singh P., Kaur A. and Kaur, P.2010. Ranking of generalized trapezoidal fuzzy numbers based on rank, mode, di-vergenceand spread. Turkish Journal of Fuzzy Systems, 1, 2: 141-152.

  19. [19] Liou, T. S. and Wang, M. J. 1992. Ranking fuzzy numbers with integral value, Fuzzy Sets and Systems, 50: 247-255.

  20. [20] Rao, P. P. B. and Shankar, N. 2011.Ranking fuzzy numbers with a distance method using circumcenter of centroidsand index of modality, Advances in Fuzzy Systems, Article, 1-7.

  21. [21] Wang, X. and Kerre, E. E. 2001. Rea-sonable properties for the ordering of fuzzy quantities (I), Fuzzy Sets and Systems,118: 375-385.

  22. [22] Wang, X. and Kerre, E. E. 2001. Rea-sonable properties for the ordering of fuzzy quantities (II), Fuzzy Sets and Systems,118: 387-405.

  23. [23] Yager, R. R. 1980. On choosing between fuzzy subsets, Kybernetes, 9:151-154.

  24. [24] Yager, R. R. 1981. A procedure for ordering fuzzy subsets of the unit interval, Information Sciences, 24: 143-161.

  25. [25] Yao, J. and Wu, K. 2000. Ranking fuzzy numbers based on decomposition princi-ple and signed distance. Fuzzy Sets and Systems, 116: 275-288.

  26. [26] Zadeh, L. A. 1965. Fuzzy sets. Information and control, 8, 3: 338-353.


ARTICLE INFORMATION

Received: 2011-08-24
Revised: 2011-09-16
Accepted: 2011-12-01
Available Online: 2012-03-01


Cite this article:

Rao, P.P.B., Shankar, N.R. 2012. Ranking generalized fuzzy numbers using Area, Mode, Spreads and weights. International Journal of Applied Science and Engineering, 10, 41–57. https://doi.org/10.6703/IJASE.2012.10(1).41

Other people also read ...

doaj logo

 

2.3
2022CiteScore
 
 
48th percentile
Powered by  Scopus
 
 

SCImago Journal & Country Rank

IJASE - Most Read Articles

IJASE - Most popular articles