D. Mallikarjuna Reddya,* and S. Swarnamani b a Mechanical Engineer, Chennai-73, India
b Mechanical Engineering Department, Indian Institute of Technology Madras, Chennai-36, India
Download Citation:
|
Download PDF
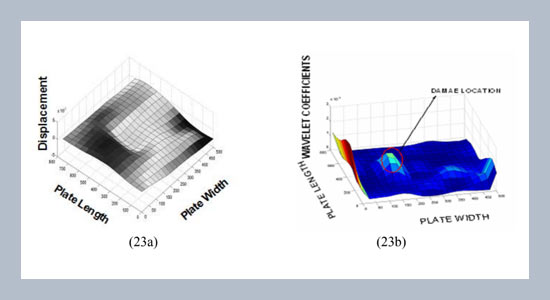
The objective of current work is to show the effectiveness of using wavelet transform for detection and localization of small damages. The spatial data used here are the mode shapes and strain energy data of the damaged plate. Because the wavelet coefficients are performed with various scale indices, local perturbations in the mode shapes and strain energy data can be found in the finer scale that are positioned at the locations of the perturbations. The continuous wavelet transform (CWT) using complex Gaussian wavelet with four vanishing moments is used to get the spatially distributed wavelet coefficients so as to identify the damage position on a square plate. The mode shape and strain energy data of the square plate with damage of different sizes are obtained by using ANSYS 9.0. The damage is simulated by reducing the thickness of one element out of 625 elements used for modeling. It is observed that by using modal data as input, damage can be identified if the reduction in thickness in one of the elements is at least 10%. Use of strain energy data as input to the wavelet analysis provides detection up to less than 10% damage. Lipschtiz (Hoelder) exponent (α) and Intensity factor (K) is derived from the coefficients to quantify the relation between damage and change in wavelet coefficients derived from modal and elemental strain energy data. The variation of maximum absolute wavelet coefficients versus percentage of damage for different mode shapes and scales are studied Influence of boundary conditions of the plate on damage identification has been studied, especially for damage near boundaries. Another objective of this paper is to apply wavelet transform to highlight the detection and localization of damage in beam and stiffened panel using experimental modal data as input to the wavelet analysis. This in real time has potential to be used in structural damage monitoring.ABSTRACT
Keywords:
Structural health monitoring; damage detection; modal analysis; spatial wavelets; lipschitz (hoelder) exponent.
Share this article with your colleagues
REFERENCES
ARTICLE INFORMATION
Received:
2011-09-01
Revised:
2011-10-14
Accepted:
2012-01-13
Available Online:
2012-03-01
Reddy, D.M., Swarnamani, S. 2012. Damage detection and identification in structures by spatial wavelet based approach. International Journal of Applied Science and Engineering, 10, 69–87. https://doi.org/10.6703/IJASE.2012.10(1).69
Cite this article: