Chi-Bin Cheng* Department of Industrial Engineering and Management, Chaoyang University of Technology, Wufeng, Taichung country 413, Taiwan, R.O.C.
Download Citation:
|
Download PDF
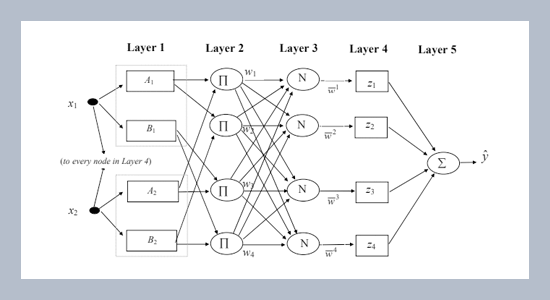
Modeling and optimization of a process with multiple outputs is discussed in this paper. A neuro-fuzzy system named MANFIS, which comprises a fuzzy inference structure and neural network learning ability, is used to model a multiple output process. Optimization of such a process is formulated as a multiple objective decision making problem, and a genetic algorithm and a numerical method are introduced, respectively, to solve this problem based on the MANFIS model. We have used these two algorithms, respectively, to solve a chemical process optimization problem, and compared their performances. A combination of these two algorithms is also suggested to improve performances of both algorithms. The proposed approach is also applied to a wire-bonding problem in semiconductor manufacturing.ABSTRACT
Keywords:
process optimization; soft computing; neuro-fuzzy system; genetic algorithm, multi-ple objective decision making; wire bonding.
Share this article with your colleagues
[1] Ames, A. E., Mattucci, N. S., MacDonald, G. Szonyi, and Hawkins, D. M. 1997. Quality loss functions for optimization across multiple response surfaces. Journal of Quality Technology, 29: 339-346.REFERENCES
[2] Cheng, C. B. 2000. Multi-response optimization based on a neuro-fuzzy system. Neural Network World, 10: 545-551.
[3] Cheng, B., Cheng, C. J., and Lee, E.S . 2002. Neuro-fuzzy and genetic algo- rithm in multiple response optimization. Computers and Mathematics with Appl-ications, 44: 1503-1514.
[4] Derringer, G. and Suich, R. 1980. Simultaneous optimization of several response variables. Journal of Quality Technology, 12: 214-219.
[5] Holland, J. H. 1975. ”Adaptation in natural and artificial systems”. University of Michigan Press, Michigan.
[6] Jang, J. S. R. ANFIS: adaptive-network-based fuzzy inference system. IEEE Transactions on Systems, Man and Cybernetics, 23: 665-684.
[7] Jang, J. S. R., Sun, C. T., and Mizutani, E. 1997. “Neuro-Fuzzy and Soft Com-puting: a Computational Approach to Learning and Machine Intelligence”. Prentice-Hall. New Jersey.
[8] Khuri, A. I. and Conlon, M. 1981. Simultaneous optimization of multiple responses represented by polynomial regression functions. Technometrics, 23: 363-375.
[9] Kim, K. J. and Lin, D. Dual response surface optimization: a fuzzy modeling approach. Journal of Quality Technology, 30: 1-10.
[10] Lin, D. and Tu, W. 1995. Dual response surface optimization. Journal of Quality Technology, 27: 34-39.
[11] Myers, R. H. and Carter, W. H. 1973. Response surface techniques for dual response systems. Technometrics, 15: 301-317.
[12] Myers, R. H. and Montgomery, D. C. 1995. “Response Surface Methodology”. John Wiley and Sons, Inc. New York.
[13] Pignatiello, J. J. Jr. 1993. Strategies for robust multiresponse quality engineering. IIE Transactions, 25: 5-15.
[14] Stone, M. 1974. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society. Series B, 36: 111-147.
[15] Takagi, T. and Sugeno, M. 1985. Fuzzy identification of systems and its applicat-ion to modeling and control. IEEE Tran-sactions on Systems, Man, and Cybernet-ics,15: 116-132.
[16] Vining, G. G. A. Compromise approach to multiresponse optimization. Journal of Quality Technology, 30: 309-313.
[17] Zimmermann, H. J. 1978. Fuzzy programming and linear programming with several objective functions. Fuzzy Sets and Systems, 1: 45-55.
ARTICLE INFORMATION
Accepted:
2003-12-23
Available Online:
2004-03-02
Cheng, C.-B., 2004. Process optimization by soft computing and its application to a wire bonding problem, International Journal of Applied Science and Engineering, 2, 59–71. https://doi.org/10.6703/IJASE.2004.2.(1).59
Cite this article: