Josyula Venkata Ramana Murthy and Meduri Phani Kumar* Department of Mathematics, National Institute of Technology, Andhra Pradesh, India
Download Citation:
|
Download PDF
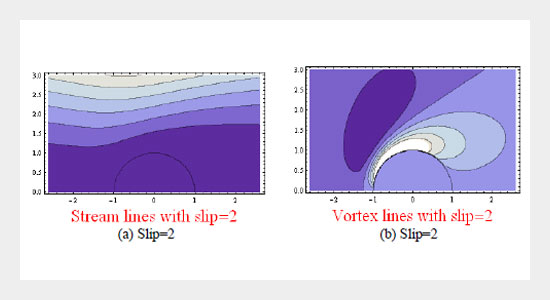
In this paper, the uniform flow of an incompressible, axi-symmetric, viscous fluid over a stationary impervious sphere with interface slip on its surface is considered. Homotopy Analysis Method (HAM) is used to solve the non linear momentum equations for stream function. To match with the uniform flow far away from the sphere, stream function is taken in terms of Gegenbauer polynomials. The solution obtained is found to be convergent and is seen to be in good agreement with the results available in literature. Drag acting on the sphere due to the flow and vorticity functions is found. For different values of the slip parameter, drag acting on the sphere is evaluated and the results are in good agreement with the available experimental data for the Reynolds numbers less than 50. Expansion of Gegenbauer polynomials and solution of the problem are obtained using MATHEMATICA.ABSTRACT
Keywords:
Slip condition; HAM; gegenbauer polynomials.
Share this article with your colleagues
[1] Knudsen, M. and Weber, S. 1911. Luftwiderstand gegen die langsame Bewegung kleiner Kugeln. Annalen der Physik, 36: 981-994.REFERENCES
[2] Millikan, R. 1923. The general law of fall of a small spherical body through a gas, and its bearing upon the nature of molecular reflection from surfaces. Physical Review, 22: 1- 23.
[3] Schaaf, S. A. and Chambre, P. L. 1961. “Flow of rarefied gases” ,Princeton University Press.
[4] Sreekanth, A. K. 1968. “Slip Flow Through Long Circular Tubes”. Rarefied Gas Dynamics, Academic Press, 667-680.
[5] Hinds, W. C. 1998. Aerosol Technology, Properties Behavior and Measurement of Airborne Particles. 2nd ed. John Wiley and Sons, New York.
[6] Gad-el-Hak, M. 1999. The fluid mechanics of microdevices-the freeman scholar lecture. Journal of Fluids Engineering, 121: 5-33.
[7] Moshfegh, A., Shams, M., Ahmadi, G., and Ebrahimi, R. 2009. A Novel Slip Correction Factor for Spherical Aerosol Particles. World Academy of Science, Engineering and Technology, 27: 709-715.
[8] Beavers, G. S. and Joseph, D. D. 1967. Boundary conditions at a naturally permeable wall. Journal of Fluid Mechanics, 30: 197-207.
[9] Saffman, P. G. 1971. On the boundary condition at the surface of a porous medium. Studies in Applied Mathematics, 2: 93-101.
[10] Crowe, C. T., Babeock, W. R., Willoughby, P. G., and Carlson, R. L. 1969. “Measurement of particle drag coefficients in flow regimes encountered by particles in a rocket nozzle”. United Technical Report 2296-FR.
[11] Gabriel, K., Jarvis, J., and Trimmer, W. 1988. Small Machines, Large Opportunities:a report on the emerging field of micro-dynamics. National Science Foundation, AT and T Bell Laboratories, Murray Hill, New Jersey, USA.
[12] Gravesen, P., Branebjerg, J., and Jenson, O. S. 1993. Microfluidics-a review. Journal of Micromechanics and Microengineering, Vol. 3: 168-182.
[13] Barber, R. W. and Emerson, D. R. 2000. A Numerical Study of Low Reynolds Number Slip Flow in the Hydrodynamic Development Region of Circular and Parallel Plate Ducts. Technical Report DL-TR-00-002, Computational Science and Engineering Department, CLRC Daresbury Laboratory.
[14] Robert Barber, W. and David Emerson, R. 2003. Numerical Simulation of Low Reynolds Number Slip Flow Past a Confined Micro-sphere. Rarefied gas dynamics, 23rd international symposium CP 663, 808-815.
[15] Luo, H. and Pozrikidis C. 2008. Effect of surface slip on Stokes flow past a spherical particle in infinite fluid and near a plane wall. Journal of Engineering Mathematics, 62: 1-21.
[16] Vinogradova, O. I. 1999. Slippage of water over hydrophobic surfaces, International Journal of Mineral Processing, 56:31-60.
[17] Tretheway, D. C. and Meinhart, C. D. 2002. Apparent fluid slip at hydrophobic micro-channel walls. Physics of Fluids, 14: L9-L12.
[18] Neto, C., Evans, D. R., Bonaccurso, E., Butt, H. J., and Craig, V. S. J. 2005. Boundary slip in Newtonian liquids: A review of experimental studies. Reports on Progress in Physics, 68, 2859-2897.
[19] Cottin-Bizonne, C., Steinberger, A., Cross, B., Raccurt, O., and Charlaix, E. 2008. Nano-hydrodynamics: The intrinsic flow boundary condition on smooth surfaces. Langmuir 24:1165-1172.
[20] Hamid Niazmand and Morteza Anbarsooz, 2012. Slip flow over micron-sized spherical particles at intermediate Reynolds numbers. Journal of Mechanical Science and Technology, 26(9): 2741-2749.
[21] Stokes, G. G., 1851. On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Cambridge Philosophical Transactions, 9: 8-106.
[22] Whitehead, A. N. 1889. A second approximation to viscous fluid motion; a sphere moving steadily in a straight line. Quarterly Journal of Mathematics, 23:143.
[23] Oseen, C. W. 1910. Arkiv. Mat. Astron. Physik., 6:29.
[24] Goldstein, S. 1929. Concerning some solutions of the boundary equations in hydrodynamics. Proceedings of the Cambridge Philosophical Society, 26.
[25] Shanks, D. 1955. Non-linear transformations of divergent and slowly convergent sequences. Journal of Mathematical Physics, 34:1.
[26] Kaplun, S. and Lagersrom, P. A. 1957. Asymptotic expansions of the Navier-Stokes solutions for small reynolds numbers. Journal of Mathematics and Mechanics, Indiana Univ. Math. J. 6 No. 4:85-593.
[27] Proudman I. and Pearson, J. R. A. 1957. Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. Journal of Fluid Mechanics, 2, Issue 03: 237-262.
[28] Van Dyke, M. 1970. Extension of Goldstein’s series for the Oseen drag of a sphere. Journal of Fluid Mechanics, Vol.44, Issue 2:365-372.
[29] Langlois, W. E. 1964. “Slow Viscous Flow”. The Macmillan Company, New York.
[30] Michaelides, E. E. 2006. Particles, Bubbles and Drops: Their Motion, Heat and Mass Transfer. Singapore: World Scientific.
[31] Dennis, S. C. R. and Walker, J. D. A. 1971. Calculation of the steady flow past a sphere at low and Moderate Reynolds numbers. Journal of Fluid Mechanics, 48,4: 771-789.
[32] Takaki, R. 2000. Flow past a sphere. SciPress, 289-325.
[33] Liao, S. J. 1999. On the viscous flow past a sphere-a simplified description. Communications in Non linear science and Numerical Simulation, 4, 2: 104-109.
[34] Liao, S. J. 2002. An analytic approximation of the drag coefficient for the viscous flow past a sphere. International Journal of Non-Linear Mechanics, 37: 1-18.
[35] Navier, M. 1823. ( Mmoire Sur les Lois du mouvement des fluides. Mmoires delAcadmie Royale des Sciences, Paris, Tome VI, 389).
[36] Maxwell, J. C. 1879. On stresses in rarefied gases arising from inequalities of temperature. Philosophical Transactions of the Royal Society, Part1, 170: 231-256.
[37] Basset, A. B. A. 1888. “Treatise on Hydrodynamics”. London: Bell.
[38] Trostel, R. Gedanken zur Konstruktion mech. Theorien II. Berlin,(TUB Forschungsbericht, Nr. 7, 1988).
[39] Atefi, G. H., Niazmand, H., and Meigounpoory, M. R. 2007. Numerical Analysis of 3-D Flow Past a Stationary Sphere with Slip Condition at Low and Moderate Reynolds Numbers. Journal of Dispersion Science and Technology, 28:591-602.
[40] Keh, H. J. and Shiau, S. C. 2000. Effects of inertia on the slow motion of aerosol particles. Chemical Engineering Science, 55: 4415-4421.
[41] Michaelides, E. E. and Feng, Z. G. 1994. The equation of motion of a small viscous ssphere in an unsteady flow with interface slip. International Journal of Multiphase Flow, 21: 315-321.
[42] Feng, Z. G. 2010. A Correlation of the Drag Force Coefficient on a Sphere with Interface Slip at Low and Intermediate Reynolds Numbers. Journal of Dispersion Science and Technology, 31, 7: 968-974.
[43] Feng, Z. G., Michaelides, E. E., and Mao, S. 2012. On the drag force of a viscous sphere with interfacial slip at small but finite Reynolds numbers. Fluid Dynamics Research, 44: 1-16.
[44] Sunil, D. and Singhal, S. 2011. Slip flow past a sphere with source at its centre. International Journal of Applied Mathematics and Mechanics, 7(6): 36-51.
[45] Miksis, M. J. and Davis, S. H. 1994. Slip over rough and coated surfaces. Journal of Fluid Mechanics, 273: 125-139.
[46] Datta, S. and Deo, S. 2002. Stokes flow with slip and Kuwabara boundary conditions. Proceedings of the Indian Academy of Sciences (Mathematical Sciences), 112, No.3: 463-475.
[47] John, H. and Howard, B. 1983. “Low Reynolds number hydrodynamics”. Martinus Nijhoff Publishers, The Hague.
[48] Liao, S. J. 2003. “Beyond Perturbation: Introduction to the Homotopy Analysis Method”. CRC Press LLC, Boca Raton.
[49] Liao, S. J. 2004. On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation, 147: 499-513.
[50] Abbasbandy, S., Shivanian, E., and Vajravelu, K. 2011. Mathematical properties of h-curve in the frame work of homotopy analysis method. Communications in Nonlinear Science and Numerical Simulation, 16: 268-4275.
[51] Oibat, Z. M. 2010. A study on the convergence of homotopy analysis method. Applied Mathematics and Computation, 217, Issue 2: 782-789.
[52] Liu, C. S. 2011. The essence of the generalized Taylor theorem as the foundation of the homotopy analysis method. Communications in Nonlinear Science and Numerical Simulation, 16: 1254-1262.
[53] Liu, C. S. 2010. The essence of homotopy analysis method. Applied Mathematics and Computation, 216, Issue 4: 1299-1303.
[54] Chester, W. and Breach, D. R. 1969. On the flow past a sphere at low Reynolds number. Journal of Fluid Mechanics, 37, part4: 751-760.
ARTICLE INFORMATION
Received:
2014-01-21
Revised:
2014-05-19
Accepted:
2014-05-22
Available Online:
2014-09-01
Murthy, J.V.R., Kumar, M.P. 2014. Effect of slip parameter on the flow of viscous fluid past an impervious sphere. International Journal of Applied Science and Engineering, 12, 203–223. https://doi.org/10.6703/IJASE.2014.12(3).203
Cite this article: