D. O. Onwuka, U. G. Eziefula*, and O. M. Ibearugbulem Department of Civil Engineering, Federal University of Technology, Owerri, Imo State, Nigeria
Download Citation:
|
Download PDF
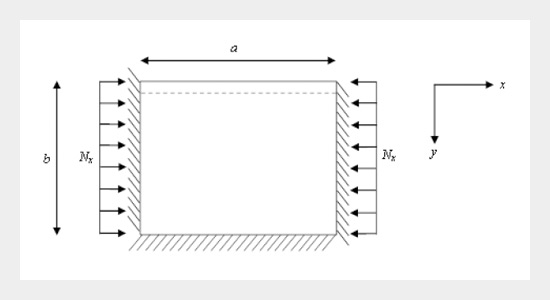
This paper presents solutions to the inelastic buckling problem of a thin flat rectangular isotropic panel under uniform uniaxial in-plane compression. The case of boundary conditions studied is a panel clamped along three edges with one simply supported longitudinal edge (CCCS). Stowell’s and Bleich’s plasticity approaches are used in deriving the governing equations. A theoretical formulation based on Taylor’s series is used in estimating the shape function which satisfied the boundary conditions and resulted to a peculiar shape function for the CCCS panel. Values of the panel buckling coefficient are calculated for aspect ratios from 0.1 to 2.0 at intervals of 0.1. The results are compared with the solutions from previous studies and the percentage differences are found to be consistent. Therefore, the proposed method can be used for the inelastic buckling analysis of thin flat rectangular isotropic panels with mixed boundary conditions subjected to uniform uniaxial in-plane loads. ABSTRACT
Keywords:
Boundary conditions; deflection function; plastic buckling; rectangular panel; Taylor’s series; variational principles.
Share this article with your colleagues
[1] Aung, J. M. 2006. “Plastic Buckling of Mindlin Plates”. Ph.D. Thesis, National University of Singapore. Singapore.REFERENCES
[2] Wang, C. M., Wang, C. Y., and Reddy, J. N. 2005. “Exact Solution for Buckling of Structural Members”. CRC Press. Boca Raton. U.S.A.
[3] Becque, J. 2010. Inelastic plate buckling. Journal of Engineering Mechanics, 136, 9: 1123-1130.
[4] Becque, J., Lathourakis, P., and Jones, R. 2011. Experimental verification of an inelastic plate theory based on plastic flow theory. Thin-Walled Structures, 49, 12: 1563-1572.
[5] Bleich, F. 1952. “Buckling Strength of Metal Structures”. McGraw-Hill. New York. U.S.A.
[6] Iyengar, N. G. R. 1988. “Structural Stability of Columns and Plates”. Ellis Horwood. Chichester. England.
[7] Shen, H.-S. 1990. Elasto-plastic analysis for the buckling and postbuckling of rectangular plates under uniaxial compression. Applied Mathematics and Mechanics, 11, 10: 931-939.
[8] Chen, Y. 2003. “Buckling of Rectangular Plates under Intermediate and End In-plane Loads”. Master Thesis, National University of Singapore. Singapore.
[9] Wang, X. and Huang, J. 2009. Elastoplastic buckling analyses of rectangular plates under biaxial loadings by the differential quadrature method. Thin-Walled Structures, 47, 1: 14-20.
[10] Maarefdoust, M. and Kadkhodayan, M. 2013. Elastoplastic buckling analysis of plates involving free edges by deformation theory of plasticity. International Journal of Engineering - Transactions A: Basics, 26, 4: 421-432.
[11] Ugural, A. C. 1999. “Stresses in Plates and Shells”, 2nd ed. McGraw-Hill. New York. U.S.A.
[12] Ventsel, E. and Krauthammer, T. 2001. “Thin Plates and Shells: Theory, Analysis and Application”. Marcel Dekker. New York.
ARTICLE INFORMATION
Received:
2015-02-02
Revised:
2016-01-01
Accepted:
2016-03-02
Available Online:
2016-03-02
Onwuka, D.O., Eziefula, U.G., Ibearugbulem, O.M. 2016. Inelastic buckling of rectangular panel with a simply supported edge and three clamped edges under uniaxial loads. International Journal of Applied Science and Engineering, 14, 39–48. https://doi.org/10.6703/IJASE.2016.14(1).39
Cite this article: